Author: Gao Huang, Zhuang Liu, Laurens van der Maaten, Kilian Q. Weinberger
Neural network 연구가 시작된 이래로 깊은 네트워크 구조를 형성하기 위한 많은 노력이 있었다. Highway Network는 bypassing path를 이용해 깊은 네트워크에서도 효율적으로 학습시키는 방법을 제안했고, ResNet이 bypassing path로 identity mapping을 사용하면서 높은 정확도를 달성하였다. 혹은 네트워크의 너비를 높이는 접근도 있었는데, GoogLeNet에서는 여러 필터를 통과시켜 결과를 concatenating하여 다음 레이어에 전달하였다. 이 연구에서는 이전의 모든 아웃풋을 현재 레이어에 인풋으로 전달함으로써 densely connected network를 형성하는 방법을 제안하였다.
Dense Connection (Dense Layer)
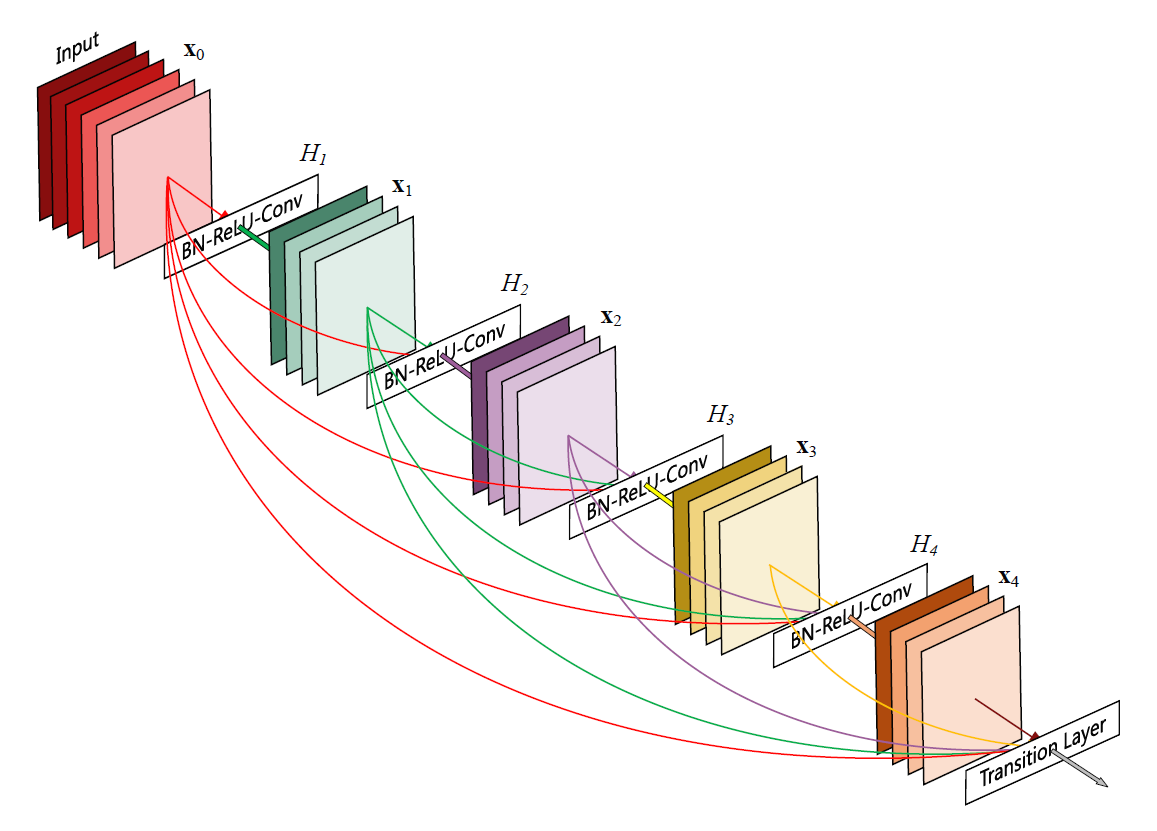
이전의 모든 레이어의 아웃풋 feature map을 concatenation 하여 현재 레이어의 input으로 넣어준다. L-layer 모델에서 첫번째 feature map은 L개 레이어에 input으로 들어가고, 두 번째 feature map은 L-1개 레이어에 전달되는 식으로 총 L(L+1)/2 개의 connection이 생성된다. 저차원의 feature map이 이후의 모든 레이어 및 loss function에 대해 직접 연결되기 때문에 모델은 저차원의 feature에 대해서도 민감해지게 된다. (모델이 깊어지더라도 저차원 feature의 변화에 대한 민감도를 반영할 수 있음).
ResNet에서도 하나의 레이어를 건너뛰어 아웃풋을 전달해주는 skip-connection 이 존재하는데, ResNet은 전달받은 아웃풋을 현재의 인풋과 element-wise로 더하는 반면 DenseNet은 concatenation하여 결합하는 방식으로 feature map을 쌓는다.
DenseNet

DenseNet은 여러 개의 Dense block으로 이루어진다. 각 block은 여러 개의 dense 레이어로 구성되어 있고, 각 레이어는 batch norm - relu - conv(3x3)로 이루어진다. 레이어 간에는 이전의 output feature map이 누적되어 다음 레이어로 전달되며, 매 레이어마다 사용하는 filter 수 만큼 feature map이 추가된다. 이 숫자를 growth rate이라고 하는데, feature map의 팽창 속도를 의미한다. 논문에서는 growth rate을 높게 설정할수록 네트워크의 성능이 더 좋아지는 것으로 확인되었다. Dense block의 마지막 레이어에서는 feature map 수가 크게 늘어난 상태이기 때문에, 다음 블록으로 넘어가기 전에 transition layer를 두어 1x1 convolution으로 feature map의 수를 줄이고 pooling으로 downsampling한다.
구현
1. Dense block 구현
normalization – activation – convolution(1x1) - normalization – activation – convolution(3x3)으로 구성되는 dense layer 클래스를 먼저 만들고, 레이어 개수를 인풋으로 받아 여러 개의 dense layer를 연결하는 DenseBlock 클래스를 생성한다.
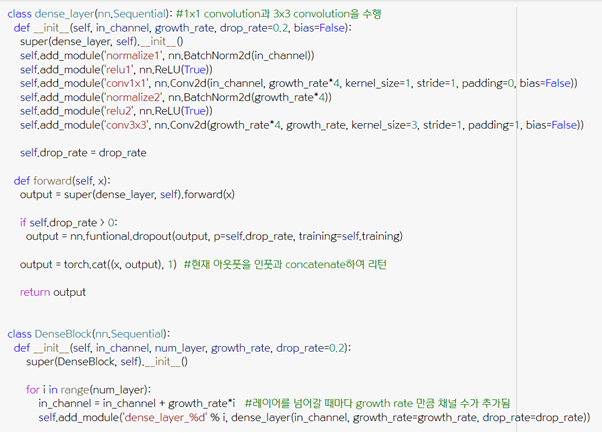
2. Transition layer 구현
Transition layer에서는 1x1 convolution으로 채널 수를 줄이고 average pooling으로 사이즈를 줄인다.

3. DenseNet-121 구현
앞서 구현한 Dense block과 transition layer 클래스를 사용해 DenseNet을 만든다. ImageNet 분류에 사용된 DenseNet121 모델은 총 4개의 dense block을 사용하는 모델이며, 블록 사이에 transition layer를 둔다. 마지막 블록 다음에는 transition layer 없이 pooling 이후 fully connected layer를 사용해 클래스 분류값을 얻어낸다.


Advantages of dense connection
1. Vanishing gradient problem을 완화시킬 수 있다.
Back propagation을 이용해 초기 레이어의 그라디언트를 계산할 때 나중 레이어들의 그라디언트가 필요하다. 여기서 activation function으로 sigmoid 함수를 사용했다면 시그모이드의 미분값은 0~0.25 사이이기 때문에 chaining을 반복할 수록(초기 레이어까지 전파할수록 시그모이드의 미분값을 여러 번 곱해주므로) 그라디언트가 작아지는 문제가 발생하였다. 그래서 RELU 함수를 사용하게 되었는데, RELU는 활성값(activated value)의 범위를 제한할 수 없다는 문제가 있지만 양수 범위에서 미분값이 항상 1이므로 여러 번 곱해주어도 그라디언트가 소멸하지 않는다.
RELU 등의 함수를 사용하더라도 레이어가 깊으면 gradient vanishing이 발생할 수 있다. 왜일까? 그라디언트의 계산식에는 activation function의 미분값 뿐 아니라 다음 레이어들의 활성화값, weight값의 미분값도 포함된다. 그러므로 weight가 0 이하의 숫자들로 이루어졌다면 그것을 곱하는 것 만으로도 그라디언트값이 줄어들고, 반복할 수록 vanishing 현상이 더 크게 발생한다.
- hackernoon.com/exploding-and-vanishing-gradient-problem-math-behind-the-truth-6bd008df6e25
- stats.stackexchange.com/questions/432300/help-understanding-vanishing-and-exploding-gradients
그런데 weight가 무엇이든 그게 그라디언트를 구하는 공식(chain rule)인데 멀어지든 말든 정확한 값이 나와야 하는 것 아닌가? - the deeper the more vanishing이라는 건 output layer와 초기 레이어 사이에 단계가 많아지기 때문에 그만큼 초기 레이어의 영향력이 줄어든다는 것. 변화에 대해 민감하지 않으니 그라디언트 자체가 작아지는 게 맞고, 초기 레이어의 영향을 output 레이어까지 가져갈 수 없다는 것을 의미. 5 hidden layer에서의 첫번째 레이어와, 50 hidden layer에서의 첫번째 레이어가 output layer에 미치는 영향을 생각해보면 당연히 후자가 적을 수 밖에 없다. 이것을 output layer에, 나아가 모든 레이어에 직접 연결해 영향력이 줄어드는 것을 해결하려고 하는 것.
"Deep Supervision" - classifier가 모든 레이어를 감시하기 때문에 네트워크가 깊어져도 이전 레이어의 feature 반영 가능.
2. Ease of feature propagation, feature reuse
이전의 feature map을 concat하여 다음 레이어에 전달하기 때문에 feature를 네트워크 전체 레이어에서 접근하여 재사용할 수 있으면서도 네트워크가 너무 깊어지지 않는다. 또한 이전에 계산된 feature를 그대로 가져와 재사용하기 때문에 다시 계산할 필요가 없다.
3. Regularization effect.
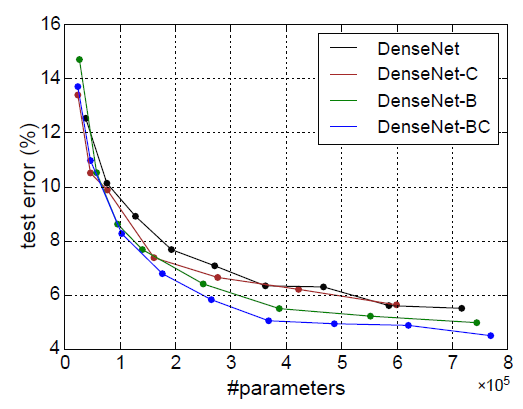
DenseNet 구조를 이용하면 레이어의 수나 필터의 개수를 늘릴수록 정확도가 높아지는 경향을 보였다. 이는 모델의 복잡도를 높여도 네트워크 구조 상 오버피팅에 빠지지 않는다는 강점을 보여준다. 이전의 feature를 사용하지 않고 레이어를 여러 개 이을수록 linear, contiguous, sequential connection을 형성하는 건데, 앞단의 feature들을 가져와서 이러한 sequential dependency를 무너트릴 수 있기 때문이 아닐까 생각해보았다.
ResNet은 data augmentation을 한 경우와 하지 않은 경우의 정확도 차이가 6%정도였는데, DenseNet은 2% 내외로 차이가 적고 augmentation을 하지 않은 상태에서도 높은 정확도를 보여주었다. 데이터의 양이 적어도 오버피팅되지 않고 regularization effect를 가짐을 알 수 있다.
4. High parameter efficiency
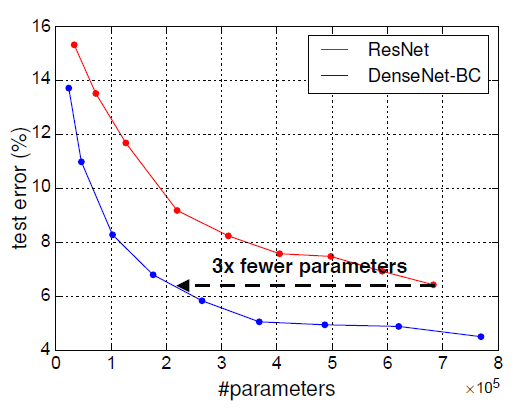
DenseNet은 당시 최고 성능을 보여주었던 ResNet과 비교해 적은 파라미터 수를 사용해 같은 성능에 도달할 수 있었다. 레이어 수가 적어도 뒤로 갈수록 많은 feature 데이터를 받아 처리하기 때문에 파라미터 사용 측면에서 효율적이라고 할 수 있다.
Feature usage heat-map

이 projection이 인상깊었다. dense block 내에서 각 레이어 별로 어떤 레이어의 아웃풋이 얼마나 영향을 미치는지 표현한 그래프이다.(average weight를 계산). diagonal line에서는 자기 자신에게 미치는 영향을 나타내기 때문에 대부분 높게 나타난다. Dense block 1의 transition layer을 보면, 초기 레이어도 많은 영향을 미치는 것을 확인할 수 있다. 그런데 Dense Block 3에서는 초기 레이어의 아웃풋보다는 나중 레이어의 아웃풋이 결과에 영향을 많이 미친다. 마지막 block에서는 고차원의 feature들이 결국 많은 영향을 미친다는 것이다. 이런 것을 확인해서 dense block을 몇 개 사용할 지 결정할 수도 있겠다는 생각이 들었다. block 1,2에서는 여전히 초기 feature도 영향을 미치기 때문에 유지해야 하고, block 3에서는 초기 feature의 영향력이 작기 때문에 이후에 dense block을 하나 더 두는 것이 큰 효용이 없을 것이다.
Q. 뒤쪽의 레이어는 고차원의 feature를 학습할텐데, 초기 레이어의 데이터를 인풋으로 보내줘도 제대로 고차원의 feature를 학습할 수 있을까?
A. dense block 단위로만 전파하기 때문에 학습하는 차원의 차이가 지나치게 크게 발생하지 않는다.
Q. relu function은 양수일 때 identity mapping으로 non-linearity를 더해줄 수 없는데 무슨 효과가 있을까?
A. 음수인 경우는 0이기 때문에 비선형이다. 그라디언트가 음수인 경우 업데이트값을 잃기 때문에 sparse network를 형성하는 효과가 있다.
'VISION' 카테고리의 다른 글
| [논문] An image is worth 16x16 words (Vision transformer) (0) | 2021.02.02 |
|---|---|
| [논문] Unpaired Image-to-Image Translation using CycleGAN (0) | 2021.01.21 |
| ideas on AI (0) | 2020.12.29 |
| 시각에 대한 생각들 (0) | 2020.11.28 |
| [강연] 컴퓨터 비전과 딥러닝의 현재와 미래 (0) | 2020.11.07 |

